
Setelah sebelumnya memposting tulisan tentang mata disini,
maka pembahasan selanjutnya tentang alat optik adalah Lup. Lup (atau
kaca pembesar), digunakan untuk memperbesar sudut pandang. Untuk
mendapatkan perbesaran maksimum benda diletakkan diruang I (antara titik
pusat optik dengan fokus f) sehingga bayangan di ruang IV didepan
lensa, semu/maya (sepihak dengan tempat benda) dan tegak.
2.1. Perbesaran Sudut (anguler)
Perbesaran Sudut (M) yaitu perbandingan antara sudut penglihatan dengan lup (θ) dan tanpa lup (θo).
Ukuran anguler
berperan dalam hal memberi kesan seberapa besar benda yang dilihat mata.
Sebagai contoh: perhatikan sebuah mobil yang bergerak mendekati kita;
ketika masih jauh mobil tersebut kelihatan kecil, tetapi semakin dekat
dengan kita, maka mobil tersebut kelihatan menjadi besar. Padahal ukuran
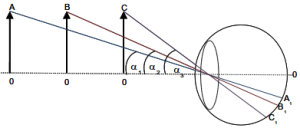
mobil yang kita lihat sebenarnya adalah tetap. Atau perhatikan diagram
benda berikut:
OA, OB dan OC adalah
benda yang sama tingginya, namun karena berbeda jaraknya, maka sudut
penglihatannya menjadi berbeda, OA yang paling jauh memiliki sudut
penglihatan yang kecil dibandingkan OB dan OC, (α1 < α2 < α3), dan
bayangan yang dibentuk diretina, OC yang paling dekat terlihat lebih
tinggi, Jadi OC1 > OB1 > OA1
Secara matematis, dari definisi diatas, perbesaran sudut M dapat dihitung dengan:
2.2. Mata Berakomodasi Maksimum
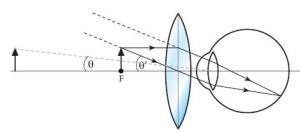
Jika seorang pengamat menggunakan lup dimana benda diletakkan antara titik O dan F (di ruang I) maka akan diperoleh bayangan yang terletak pada titik dekat mata pengamat (s’ = sn). Karena sudut pandang mata menjadi lebih besar, maka mata pengamat berakomodasi maksimum.
Jadi, untuk mata berakomodasi maksimum, bayangan yang dihasilkan lup harus terletak dititik dekat mata. Sehingga bayangannya, S’ = – Sn,
oleh karena itu, perbesaran bayangan pada lup (M) merupakan
perbandingan antara letak bayangan (s’) dengan letak benda (s), karena
s’ = – 25 cm (tanda negatif menunjukkan bahwa bayangan jatuh didepan
lensa).
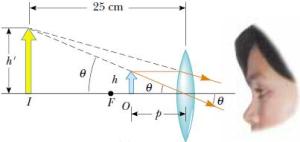
Perhatikan gambar berikut:
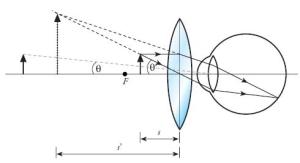
Perhatikan gambar berikut:

Perbesaran sudut dapat dihitung dengan persamaan berikut:
2.3. Mata Tidak Berakomodasi
Untuk mata tidak berakomodasi (supaya mata tidak cepat lelah), maka benda (S) diletakkan pada titik fokus lensa (lup), sehingga bayangan akan diperbesar dan jatuh di jauh tak berhingga, sehingga S’ = ~ dan S = f
Dari hal ini
diperoleh bahwa sudut penglihatan tanpa menggunakan lup merupakan
perbandingan tinggi benda (h) dengan jarak titik dekat mata (Sn).
Sehingga perbesaran sudut untuk penglihatan menggunakan lup tanpa berakomodasi dapat dihitung dengan persamaan:
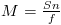 ………………………… (3)
………………………… (3)
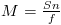 ………………………… (3)
………………………… (3)
2.4. Mata Berakomodasi Pada Jarak x
Untuk mata berakomodasi pada jarak x, artinya bayangan yang dibentuk oleh lensa jatuh pada jarak x di depan mata (S’ = – x), sehingga perbesaran lup adalah:
 ………………………… (4)
………………………… (4)
 ………………………… (4)
………………………… (4)
2.5. Mata Berakomodasi Pada Jarak x dan Lup Tidak Menempel Pada Mata.
Untuk mata berakomodasi pada jarak x, dan mata mempunyai jarak d dari lup, maka perbesaran yang dihasilkan adalah:
 ………………………… (5)
………………………… (5)
 ………………………… (5)
………………………… (5)
Contoh Soal 1:
Seorang tukang jam
menggunakan lup yang berkekuatan 8 dioptri, dimanakah letak benda dan
perbesaran anguler yang diperoleh jika mata tukang jam tersebut
a.Berakomodasi maksimum
b.Tidak berakomodasi (titik jauh dekat pengamat 25 cm)
a.Berakomodasi maksimum
b.Tidak berakomodasi (titik jauh dekat pengamat 25 cm)
Petunjuk Jawaban:
Hitung terlebih dahulu fokus lensa dengan persamaan

sehingga didapat fokus lensa = 12,5 cm (jawaban)
Hitung terlebih dahulu fokus lensa dengan persamaan

sehingga didapat fokus lensa = 12,5 cm (jawaban)
a. Untuk mata berakomodasi maksimum,
maka S’ = – Sn = – 25 cm; dan dari perhitungan diatas didapat f = 12,5 cm
Dengan menggunakan persamaan lensa tipis yaitu:
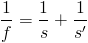
maka diperoleh letak benda, S = 25/3 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (2), yaitu:

maka akan didapatkan perbesaran sudutnya adalah : M = 3 kali (jawaban)
maka S’ = – Sn = – 25 cm; dan dari perhitungan diatas didapat f = 12,5 cm
Dengan menggunakan persamaan lensa tipis yaitu:
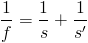
maka diperoleh letak benda, S = 25/3 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (2), yaitu:

maka akan didapatkan perbesaran sudutnya adalah : M = 3 kali (jawaban)
b.Mata tidak berakomodasi
Titik jauh pengamat ada di tak berhingga, maka benda terletak didepan lensa dan di titik fokus, maka
S = f = 12,5 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3):
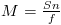
maka didapat perbesaran sudutnya M = 2 (jawaban)
Titik jauh pengamat ada di tak berhingga, maka benda terletak didepan lensa dan di titik fokus, maka
S = f = 12,5 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3):
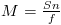
maka didapat perbesaran sudutnya M = 2 (jawaban)
Contoh Soal 2:
Seorang tukang jam
menggunakan lup yang berkekuatan 8 dioptri, dimanakah letak benda dan
perbesaran anguler yang diperoleh jika mata tukang jam tersebut
berakomodasi pada jarak 50 cm.
Petunjuk Jawaban:
Hitung terlebih dahulu fokus lensa
Didapat fokus lensa = 12,5 cm
Hitung terlebih dahulu fokus lensa
Didapat fokus lensa = 12,5 cm
Contoh Soal 3:
Sebuah lup berkekuatan
20 dioptri, dimanakah letak benda dan perbesaran anguler yang diperoleh
jika pengamat yang menggunakan lup tersebut tidak berakomodasi, dan
mempunyai titik dekat 30 cm dan titik jauhnya 2 meter.
Petunjuk Jawaban:
Hitung terlebih dahulu fokus lensa, dan didapat fokus lensa = 5,0 cm .
Hitung terlebih dahulu fokus lensa, dan didapat fokus lensa = 5,0 cm .
Karena titik jauh pengamat 2,00 m bukan
di titik jauh tak hingga, maka bayangan lensa harus terletak di depan
lensa pada jarak titik jauh pengamat, jadi S’ = – 200 cm.
Dengan menggunakan persamaan lensa tipis, maka diperoleh letak benda, S = 200/41 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3)
maka didapat perbesaran sudutnya adalah M = 6,15 (jawaban)
Dengan menggunakan persamaan lensa tipis, maka diperoleh letak benda, S = 200/41 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3)
maka didapat perbesaran sudutnya adalah M = 6,15 (jawaban)
- Seorang bermata normal memakai lup yang kekuatannya 20 dioptri. Hitung perbesaran sudutnya jika : (a) a.mata berakomodasi maksimum dan (b) mata tak berakomodasi
- Seseorang bermata normal mengamati benda dengan sebuah lup yang kuatnya 18 dioptri. Berapakah perbesaran sudutnya jika: (a). mata berakomodasi maksimum; (b). mata tidak berakomodasi; (c). mata berakomodasi pada jarak 80 cm; dan (d). mata berakomodasi pada jarak 80 cm tetapi mata menjauh sebesar 2 cm
- Seseorang menggunakan lup yang kekuatannya 4 dioptri. Sebuah benda yang tingginya 2 cm diamati oleh orang tersebut. Berapakah tinggi bayangan yang dilihat jika: (a). benda terletak pada jarak 24 cm dan (b). benda terletak pada jarak 25 cm
- Sebuah benda diletakkan didepan lensa cembung sejauh 5,00 cm dan terbentuk bayangan nyata pada jarak 20,0 cm dari lensa. Jika lensa digunakan sebagai lup, tentukanlah perbesaran anguler lup, untuk: (a). Mata berakomodasi pada jarak 40 cm dan (b). Mata tidak berakomodasi
- Seseorang memiliki titik dekat 27 cm, melihat bayangan sebuah benda dengan lup diperbesar 10 kali saat ia melihatnya dengan berakomodasi sekuat-sekuatnya. (a). Tentukan fokus lup dan kekuatanya dan (b). Kemana benda harus digeser dan berapa jauhnya, agar perbesaran sudutnya menjadi 9,75 kali


Tidak ada komentar:
Posting Komentar